|
|
|
1.
|
Find real numbers a and b such that
the equation is true.
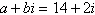
|
|
|
2.
|
Perform the addition or subtraction and write the
result in standard form.
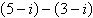
a. | 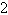 | b. | 4 | c. | 6 | d. | 5 | e. | 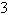 |
|
|
|
3.
|
Write the quotient in standard form.
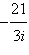
|
|
|
4.
|
Simplify the complex number and write it in
standard form.
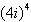
|
|
|
5.
|
Determine the number of solutions of the equation
in the complex number system.
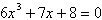
a. |  has degree 6 so there are
three solutions in the complex number system. has degree 6 so there are
three solutions in the complex number system. | b. | 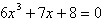 has degree 3 so there are three solutions in the complex number system.
has degree 3 so there are three solutions in the complex number system. | c. | 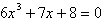 has degree 7 so there are no solutions in the
complex number system. has degree 7 so there are no solutions in the
complex number system. | d. |  has degree 6 so there are no solutions in the complex number system.
has degree 6 so there are no solutions in the complex number system. | e. | 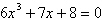 has degree 7 so there are three solutions in
the complex number system. has degree 7 so there are three solutions in
the complex number system. |
|
|
|
6.
|
Find all the zeros of the function and write the
polynomial as a product of linear factors.
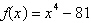
|
|
|
7.
|
Use the given zero to find all the zeros of the
function.
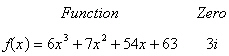
|
|
|
8.
|
Solve the equation and write complex solutions in
standard form.
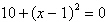
|
|
|
9.
|
Given that 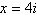 is a zero of is a zero of
 , find all the zeros
of f. , find all the zeros
of f.
|
|
|
10.
|
Plot the complex number
and find its absolute value.
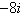
|
|
|
11.
|
Perform the operation
and leave the result in trigonometric form.
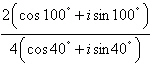
|
|
|
12.
|
Find the trigonometric form of 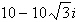 . .
|
|
|
13.
|
Multiply the complex numbers. Write the answer in
trigonometric form.
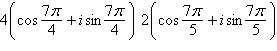
a. | 8 cos 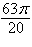 | b. | 8 cos 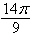 | c. | 8 cos 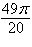 | d. | 6 cos 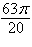 | e. | 6 cos 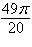 |
|
|
|
14.
|
Multiply the complex numbers. Write the answer in
trigonometric form.
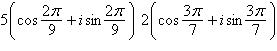
a. | 7 cos 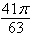 | b. | 10 cos 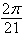 | c. | 7 cos 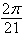 | d. | 10 cos 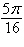 | e. | 10 cos 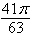 |
|
|
|
15.
|
Use DeMoivre’s Theorem to find the indicated
power of the complex number. Write the result in standard form.
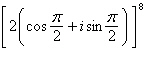
|
|
|
16.
|
Use DeMoivre’s Theorem to find the indicated
power of the complex number. Write the result in standard form.
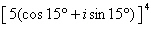
|
|
|
17.
|
Use DeMoivre’s theorem to find all the
solutions of the equation and represent the solutions graphically. (Round your answer to four decimal
places.)
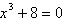
|
|
|
18.
|
Use DeMoivre’s theorem to find all the
solutions of the equation and represent the solutions graphically. (Round your answer to four decimal
places.)
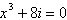
|
|
|
19.
|
Write the following roots in standard form. (Round
your answer to four decimal places.)
Cube roots of 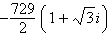
|
|
|
20.
|
Use DeMoivre's Theorem to find the indicated
power of the complex number. Write the result in standard form.
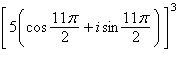
|