|
|
|
1.
|
The given points represent the vertices of a
triangle.Select the triangle ABC in the coordinate plane.

|
|
|
2.
|
Find the vertex, focus, and directrix of the
parabola.
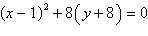
|
|
|
3.
|
The revenue R (in dollars) generated by the
sale of x units of a digital camera is given by
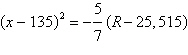 . .
Approximate the number
of sales that will maximize revenue.
a. | Maximum revenue occurs at  units.
units. | b. | Maximum revenue occurs at  units.
units. | c. | Maximum revenue occurs at  units.
units. | d. | Maximum revenue occurs at  units.
units. | e. | Maximum revenue occurs at 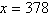 units.
units. |
|
|
|
4.
|
Find the center, vertices and foci of the
hyperbola.

|
|
|
5.
|
The 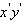 -coordinate system has been rotated -coordinate system has been rotated 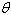 degrees from the degrees from the 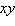 -coordinate system. The coordinates of a point in the -coordinate system. The coordinates of a point in the 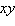 -coordinate
system are given. Find the coordinates of the point in the rotated coordinate system. -coordinate
system are given. Find the coordinates of the point in the rotated coordinate system.
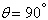 , , 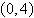
|
|
|
6.
|
Select the graph of the following equation, showing
both sets of axes.

|
|
|
7.
|
Use the discriminant to
classify the graph.
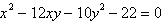
a. | The graph is a parabola. | b. | The graph is a hyperbola. | c. | The graph is a ellipse. | d. | The graph is a
cone. | e. | The graph is a
circle. |
|
|
|
8.
|
Select the parametric equations matching with the
following graph.

|
|
|
9.
|
Convert the rectangular equation to polar form.
Assume 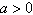 . .
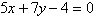
|
|
|
10.
|
Convert the rectangular equation to polar form.
Assume  . .
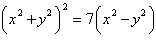
|
|
|
11.
|
Convert the rectangular equation to polar form.
Assume 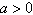 . .
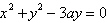
|
|
|
12.
|
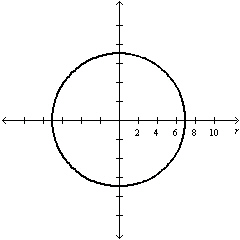
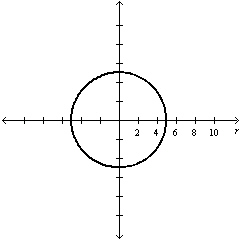
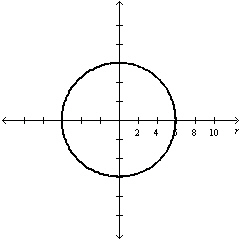
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
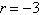
a. | Symmetric with respect to  , polar axis,
pole , polar axis,
pole
Circle with radius 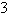
 | d. | Symmetric with respect to  , polar
axis, pole , polar
axis, pole
Circle with radius 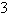
 | b. | Symmetric with
respect to 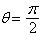 , polar axis, pole , polar axis, pole
Circle with radius 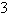
 | e. | Symmetric with
respect to  , polar axis, pole , polar axis, pole
Circle with radius 
 | c. | Symmetric with respect to 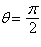 , polar axis, pole , polar axis, pole
Circle
with radius 
 |
|
|
|
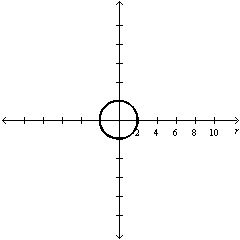
13.
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
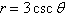
|
|
|
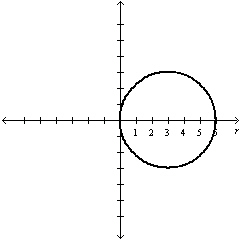
14.
|
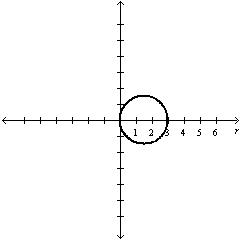
Select the graph of  over the
interval. Describe the part of the graph obtained in this case. over the
interval. Describe the part of the graph obtained in this case.
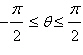
a. |
Entire
circle | d. |
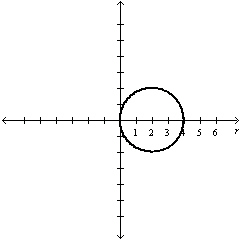
Entire
circle | b. |
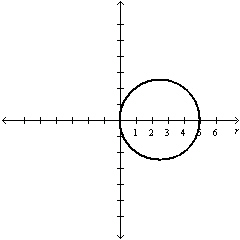
Entire
circle | e. |
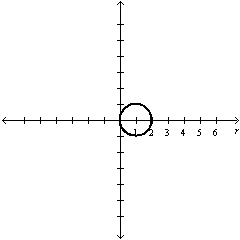
Entire circle | c. |
Entire
circle |
|
|
|
15.
|
Select the graph of the equation.

|
|
|
16.
|
Select the correct graph of the polar equation.
Find an interval for 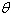 for which the graph is traced only
once. for which the graph is traced only
once.
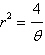
|
|
|
17.
|
Find a polar equation of the conic with its focus
at the pole.

|
|
|
18.
|
Identify the conic and select its correct
graph.
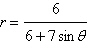
|
|
|
19.
|
Select correct graph to graph rotated
conic.
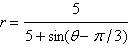
|
|
|
20.
|
A satellite in a 100-mile-high circular orbit
around Earth has a velocity of approximately 17,500 miles per hour. If this velocity is multiplied by
 , the satellite will have the minimum velocity
necessary to escape Earth’s gravity and will follow a parabolic path with the center of Earth
as the focus. (Hints: The radius of Earth is 4000 miles.) , the satellite will have the minimum velocity
necessary to escape Earth’s gravity and will follow a parabolic path with the center of Earth
as the focus. (Hints: The radius of Earth is 4000 miles.)

Find the
distance between the surface of the Earth and the satellite when  . .
a. | Distance between surface of Earth and satellite:110
miles | b. | Distance between surface of Earth and satellite:105
miles | c. | Distance between surface of Earth and satellite:120
miles | d. | Distance between surface of Earth and satellite:100
miles | e. | Distance between surface of Earth and satellite:102
miles |
|