|
|
|
1.
|
Find the inclination 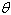 (in degrees)
of the line with a slope of (in degrees)
of the line with a slope of 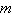 . Round your answer to one decimal
places. . Round your answer to one decimal
places.
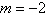
|
|
|
2.
|
Find the inclination 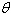 (in degrees)
of the line with a slope of (in degrees)
of the line with a slope of 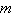 . Round your answer to one decimal
places. . Round your answer to one decimal
places.
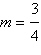
|
|
|
3.
|
Find the standard form of the equation of the
parabola with the given characteristics.
Vertex:  ; directrix: ; directrix: 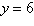
|
|
|
4.
|
The revenue R (in dollars) generated by the
sale of x units of a patio furniture set is given by
 . .
Select
the correct graph of the function.
|
|
|
5.
|
Find the standard form
of the equation of the ellipse with the given characteristics and center at the
origin.
Vertices: 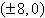 ; Foci: ; Foci: 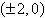
|
|
|
6.
|
Find the vertices of
the conic.
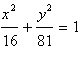
a. | Vertices: 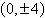 | b. | Vertices: 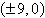 | c. | Vertices:  | d. | Vertices:  | e. | Vertices: 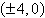 |
|
|
|
7.
|
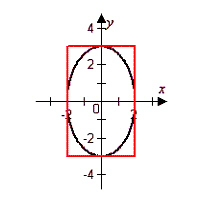
An elliptical stained-glass insert is to be fitted
in a
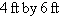
rectangular opening (see figure). Using
the coordinate system shown, find an equation for the ellipse.
|
|
|
8.
|
Find the center, vertices and foci of the
hyperbola.

|
|
|
9.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
Vertices: (4,0),(8,0); foci: (0,0),
(10,0)
|
|
|
10.
|
Select the graph of the equation as a circle, a
parabola, an ellipse, or a hyperbola.
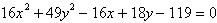
a. | Parabola | b. | Circle | c. | Hyperbola | d. | Ellipse | e. | None of the
above |
|
|
|
11.
|
Rotate the axes to eliminate the xy-term in
the equation. Then write the equation in standard form.

|
|
|
12.
|
Use the Quadratic
Formula to solve for 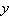 . .
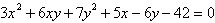
|
|
|
13.
|
Consider the
equation.
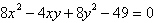
Without
calculating, explain how to rewrite the equation so that it does not have an  -term. -term.
|
|
|
14.
|
A point (a,b) shown in below
graph in polar coordinates is given. Convert the point to rectangular coordinates.

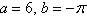
|
|
|
15.
|
A point in rectangular coordinates is given.
Convert the point to polar coordinates.
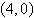
|
|
|
16.
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
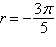
a. | Symmetric with respect to  , polar axis,
pole , polar axis,
pole
Circle with radius 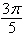
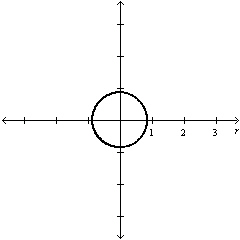 | d. | Symmetric with respect to 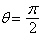 , polar
axis, pole , polar
axis, pole
Circle with radius 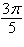
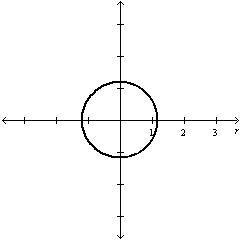 | b. | Symmetric with
respect to 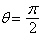 , polar axis, pole , polar axis, pole
Circle with radius 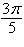
 | e. | Symmetric with
respect to 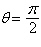 , polar axis, pole , polar axis, pole
Circle with radius 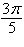
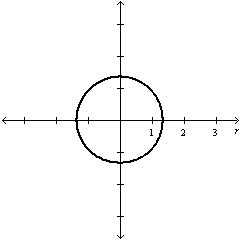 | c. | Symmetric with respect to 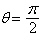 , polar axis, pole , polar axis, pole
Circle
with radius 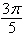
 |
|
|
|
17.
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
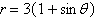
|
|
|
18.
|
Select the correct graph of the polar equation.
Find an interval for 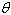 for which the graph is traced only
once. for which the graph is traced only
once.

|
|
|
19.
|
Find a polar equation of the conic with its focus
at the pole.
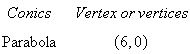
|
|
|
20.
|
The comet Hale-Bopp has an elliptical orbit with an
eccentricity of 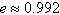 .The length of the major axis of the orbit is
approximately 504 astronomical units. Find a polar equation for the orbit. How close does the comet
come to the sun? .The length of the major axis of the orbit is
approximately 504 astronomical units. Find a polar equation for the orbit. How close does the comet
come to the sun?
|