|
|
|
1.
|
Select the graph of the exponential function. 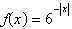
|
|
|
2.
|
Select the graph of the exponential function. 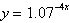
|
|
|
3.
|
Determine whether the statement is true or false. Justify your
answer. The line 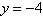 is an asymptote for the graph of 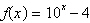
|
|
|
4.
|
Write the exponential equation in logarithmic form. 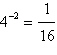
|
|
|
5.
|
Rewrite the logarithm as a ratio of natural logarithms. 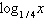
|
|
|
6.
|
Use the properties of logarithms to expand the expression as a sum, difference,
and/or constant multiple of logarithms. (Assume all variables are positive.) 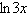
|
|
|
7.
|
Use a graphing utility to graph the functions given by 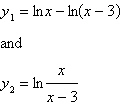 in the same viewing window.
|
|
|
8.
|
Evaluate the logarithm using the change-of-base formula. Round your result to
three decimal places. 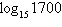
|
|
|
9.
|
Use the properties of logarithms to rewrite and simplify the logarithmic
expression. 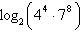
|
|
|
10.
|
Find the exact value of 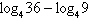 without using a
calculator. a. | 1 | b. | 4 | c. | 9 | d. | 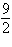 | e. | 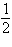 |
|
|
|
11.
|
Condense the expression 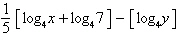 to the logarithm of a single
term.
|
|
|
12.
|
Approximate the point of intersection of the graphs of f and g.
Then solve the equation 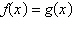 algebraically to verify your
approximation. 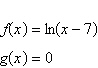 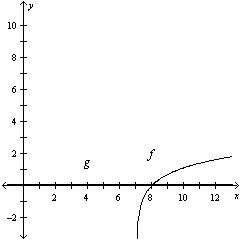
|
|
|
13.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 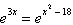
|
|
|
14.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 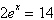
|
|
|
15.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 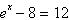
|
|
|
16.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 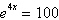
|
|
|
17.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 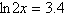
|
|
|
18.
|
Solve for x: 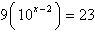 . Round to 3 decimal places. a. | 0.407 | b. | –1.362 | c. | 1.362 | d. | 2.407 | e. | no
solution |
|
|
|
19.
|
Select the correct graph for the given function 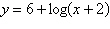
|
|
|
20.
|
Find the exponential model that  fits the points shown in the
graph. 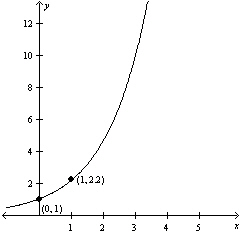
|