|
|
|
1.
|
Select the graph of the function. 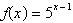
|
|
|
2.
|
Evaluate the function at the indicated value of 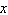 . Round your
result to three decimal places.
Function
Value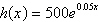
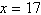
|
|
|
3.
|
Select the graph of the function. 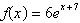
|
|
|
4.
|
Select the graph of the exponential function. 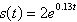
|
|
|
5.
|
Select the graph of the exponential function. 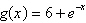
|
|
|
6.
|
Use the One-to-One Property to solve the equation for 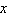 . 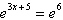
|
|
|
7.
|
Use the One-to-One Property to solve the following equation for
x. 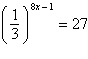
|
|
|
8.
|
Select the graph of the function. 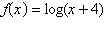
|
|
|
9.
|
Rewrite the logarithm as a ratio of common logarithms. 
|
|
|
10.
|
Determine whether the statement is true or false given that 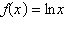 . 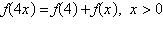
|
|
|
11.
|
Evaluate the logarithm using the change-of-base formula. Round your result to
three decimal places. 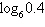
|
|
|
12.
|
Solve for 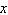 . Approximate the result to three decimal
places. 
|
|
|
13.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 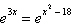
|
|
|
14.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 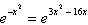
|
|
|
15.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 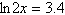
|
|
|
16.
|
Select the correct graph for the given function 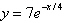
|
|
|
17.
|
Select the correct graph for the given function 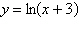
|
|
|
18.
|
Complete the table for a savings account in which interest is compounded
continuously. Initial investment | Annual rate | Time to double | Amount after 10 years | | --- | --- | | | | | |
(Round the answer upto
two decimal places.)
|
|
|
19.
|
The populations P (in thousands) of Orlando, Florida from 2000 through
2007 can be modeled by 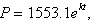 where t represents the year, with 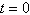 corresponding to 2000. In 2005, the population of Orlando, Florida was about 1,902,000.
Find the value of k.
|
|
|
20.
|
The chemical acidity of a solution is measured in units of pH: 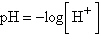 ,
where 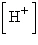 is the hydrogen ion concentration in the
solution. If a sample of rain has a pH of 3.2, how many times higher is its 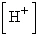
than pure water's, which has a pH of 7?
|