|
|
|
1.
|
Use the Law of Sines to
solve (if possible) the triangle. Round your answers to two decimal places.
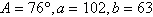
|
|
|
2.
|
Find values for 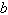 such that the
triangle has one solution. such that the
triangle has one solution.
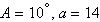
|
|
|
3.
|
Find values for 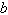 such that the
triangle has two solutions. such that the
triangle has two solutions.
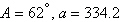
|
|
|
4.
|
Because of prevailing
winds, a tree grew so that it was leaning  from the vertical. At a
point from the vertical. At a
point 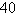 meters from the tree, the angle of elevation
to the top of the tree is meters from the tree, the angle of elevation
to the top of the tree is 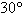 (see figure). Find the height (see figure). Find the height  of the tree.
of the tree.
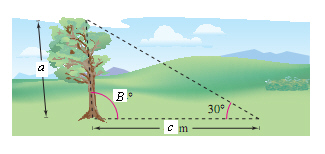
where 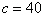 m
m
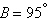
(Round
your answer to two decimal places.)
|
|
|
5.
|
Use the low of Cosines to solve the given triangle.
Round your answer to two decimal places.
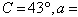  , b = , b =
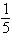
|
|
|
6.
|
Use the Heron’s formula to find the area of
the triangle. Round your answer upto two decimal places.
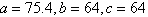
|
|
|
7.
|
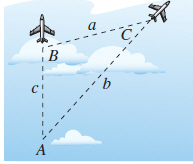
To determine the distance between two aircraft, a
tracking station continuously determines the distance to each aircraft and the angle  between them (see figure). Determine the distance a between the planes when A=
between them (see figure). Determine the distance a between the planes when A=  miles, b= miles, b= 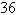 miles, and c= miles, and c= 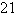 miles. miles.
a. | 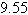 miles miles | b. | 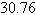 miles
miles | c. | 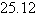 miles miles | d. |  miles
miles | e. | 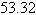 miles miles |
|
|
|
8.
|
The initial and terminal points of a vector are
given. Select a linear combination of the standard unit vectors i and
j.
Initial
Point | Terminal Point | | | | |
|
|
|
9.
|
A force of F pounds is required to pull an
object weighing W pounds up a ramp inclined at  degrees from the
horizontal. degrees from the
horizontal.
Find F if 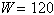 pounds and pounds and 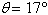 . .
a. | 33.1 lb | b. | 36.1 lb | c. | 35.1
lb | d. | 37.1 lb | e. | 34.1 lb |
|
|
|
10.
|
A loaded barge is being towed by two tugboats, and
the magnitude of the resultant is 6300 pounds directed along the axis of the barge (see figure). Find
the tension in the tow lines if they each make an angle 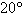 with the axis of the
barge. with the axis of the
barge.
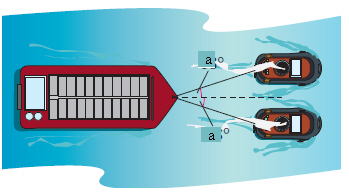
where 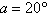
a. | 3350.2 lb | b. | 3354.2 lb | c. | 3351.2
lb | d. | 3353.2 lb | e. | 3352.2 lb |
|
|
|
11.
|
Using the figure below, sketch a graph of the given
vector. [The graphs in the answer choices are drawn to the same scale as the graph
below.]
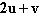
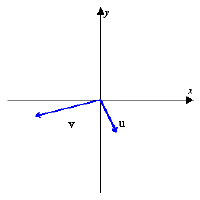
|
|
|
12.
|
Find a unit vector in the direction of 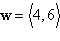 . .
|
|
|
13.
|
Let w be a vector with initial point 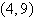 and terminal point and terminal point 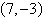 . Write w as a linear combination of the
standard unit vectors i and j. . Write w as a linear combination of the
standard unit vectors i and j.
|
|
|
14.
|
Find the component form of v if 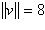 and the angle it makes with the x-axis is 150°. and the angle it makes with the x-axis is 150°.
|
|
|
15.
|
Three forces with magnitudes of 84 pounds, 83
pounds, and 135 pounds act on an object at angles 160°, 200°, and 280°, respectively,
with the positive x-axis. Find the magnitude and direction of the resultant force. Round
answers to two decimal places.
a. | 188.16 pounds; 224.81° | b. | 169.82 pounds; 224.81° | c. | 188.16 pounds; 44.81° | d. | 169.82 pounds; 44.81° | e. | 209.87 pounds; 256.33° |
|
|
|
16.
|
Use the vectors  to find
the indicated quantity. State whether the result is a vector or a scalar. to find
the indicated quantity. State whether the result is a vector or a scalar.
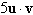
a. | 30; scalar | b. | 28; scalar | c. | 32;
scalar | d. |  ;
vector ;
vector | e. | 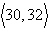 ;
vector ;
vector |
|
|
|
17.
|
Use the dot product to find the magnitude of
u.
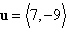
|
|
|
18.
|
Find the projection of u onto
v.
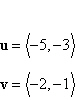
|
|
|
19.
|
|
|
|
20.
|
Determine whether u are v and
orthogonal, parallel, or neither.
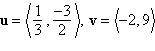
a. | neither | b. | parallel | c. | orthogonal |
|