Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
directrix: x =
1
a. | x2 =
–4y | b. | y2 = –4x | c. | x2 = 4y | d. | x2 = y | e. | y2 = x |
|
|
|
2.
|
Find the vertex and focus of the parabola.
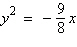
a. | vertex: 
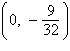focus:  | b. | vertex:  focus: 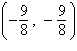 | c. | vertex: (0,
0) focus: 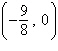 | d. | vertex: (0, 0) focus: 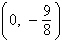 | e. | vertex: (0,
0) focus:  |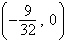
|
|
|
3.
|
Find the vertex and directrix of the
parabola.
|
|
|
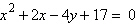
4.
|
Give the standard form of the equation of the
parabola with the given characteristics.
vertex: (–3,
1) focus: (–1, 1)
|
|
|
5.
|
As a speeding train crosses a trestle over a deep
gorge, a child drops his toy plane from the window. The path of the toy plane is modeled by  , where y is the height above the floor of the gorge and distances are measured in
feet. How far will the toy plane travel horizontally before it hits the bottom of the gorge?
[Note: The toy plane does not glide; it "drops like a
rock."]
a. | 900 ft | b. | 120 ft | c. | 30 ft | d. | 11 ft | e. | 7.5 ft |
|
|
|
6.
|
An elliptical stained-glass insert is to be fitted
in a
rectangular opening (see figure). Using
the coordinate system shown, find an equation for the ellipse.
|
|
|
7.
|
Find the standard form of the equation of the
ellipse with the following characteristics.
foci: 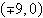 | major axis of length: 20 | | |
|
|
|
8.
|
Find the standard form of the equation of the
ellipse with the following characteristics.
foci:  major axis of length:
12
|
|
|
9.
|
Find the center and vertices of the
ellipse.
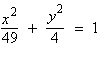
a. | center: (7,
0) vertices: (0, –2), (0,
2) | b. | center: (7,
2) vertices: (–7, –2), (7,
2) | c. | center: (0,
0) vertices: (0, –7), (0,
7) | d. | center: (0,
0) vertices: (–7, 0), (7,
0) | e. | center: (0,
0) vertices: (–2, 0), (2,
0) |
|
|
|
10.
|
Identify the conic by writing the equation in
standard form.
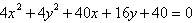
a. |  ;
ellipse | b. |  ;
circle | c. |  ;
circle | d. |  ;
circle | e. |  ;
ellipse |
|
|
|
11.
|
Find the center and vertices of the
ellipse.
|
|
|
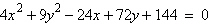
12.
|
Find the center and vertices of the ellipse.
 = 0
a. | center: (3, –8)
vertices: (0, –8), (6, –8) | b. | center: (8, –3)
vertices: (5, –3), (11, –3) | c. | center: (–8, 3)
vertices: (–11, 3), (–5, 3) | d. | center: (–8, 3)
vertices: (–9, 3), (–7, 3) | e. | center: (8, –3)
vertices: (7, –3), (9,
–3) |
|
|
|
13.
|
Find the vertices and asymptotes of the
hyperbola.
|
|
|
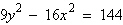
14.
|
Find the vertices and asymptotes of the
hyperbola.
|
|
|
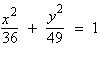
15.
|
Find the center and foci of the
hyperbola.
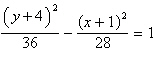
a. | center: (1, 4), foci: (1, –4), (1,
12) | b. | center: (–1, –4), foci: (–1,
–12), (–1, 4) | c. | center: (4, 1),
foci: (4, –7), (4, 9) | d. | center: (–4,
–1), foci: (–12, –1), (4, –1) | e. | center: (–1, –4), foci: (–9, –4), (7,
–4) |
|
|
|
16.
|
Find the center and vertices of the
hyperbola.
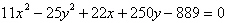
a. | center: (1,–5), vertices: (–4, –5),
(6, –5) | b. | center: (–5,
1), vertices: (–10, 1), (0, 1) | c. | center: (–1,
5), vertices: (–1, 0), (–1, 10) | d. | center: (–1,
5), vertices: (–6, 5), (4,5) | e. | center: (1,
–5), vertices: (1, –10), (1, 0) |
|
|
|
17.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
vertices:  foci: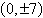 
|
|
|
18.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
| vertices: (–2, –4), (–2, 6) | foci: (–2, –5), (–2,
7) | | |
|
|
|
19.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
foci:  asymptotes: 
|
|
|
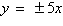
20.
|
A pinball machine is designed so that a bumper on
one side is hyperbolic in shape. If a pinball is directed at its focus, the ball will be reflected to
a 10,000 point bonus pocket positioned at the other focus (see figure). If the focus of the bumper
has coordinates (8, 0), and the vertex of the bumper is (6, 0), find the standard form of the
equation that models the shape of the bumper.
|
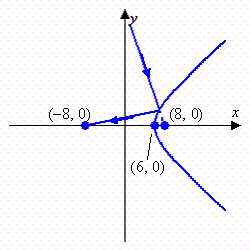