|
|
|
1.
|
Graphically estimate the x- and
y-intercepts of the graph.
|
|
|
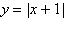
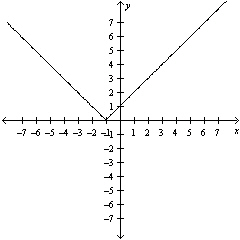
2.
|
Identify any intercepts and test for symmetry. Then
sketch the graph of the equation.
|
|
|
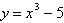
3.
|
Write the standard form of the equation of the
circle with the given characteristics.
center:  ; solution point: 
|
|
|
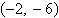
4.
|
Determine whether the value of 
is a solution of the equation.
|
|
|
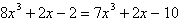
5.
|
Solve the equation and check your
solution.
|
|
|
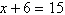
6.
|
Solve the equation for  . (Round your
answer to three decimal places.)
|
|
|
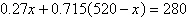
7.
|
Write the following quadratic equation in standard
form.
|
|
|
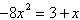
8.
|
Solve the equation  by extracting
square roots.
|
|
|
9.
|
Use the Quadratic Formula to solve  .
|
|
|
10.
|
The floor of a one-story building is 14 feet longer
than it is wide (see figure). The building
has 2760 square feet of floor space.
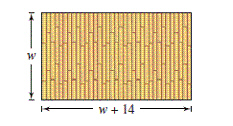
Write a quadratic equation for the area of the floor in terms of 
and find the length and width of the floor.
|
|
|
11.
|
Write the quotient in standard form.
|
|
|
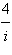
12.
|
Simplify the complex number and write it in
standard form.
|
|
|
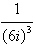
13.
|
Raise each complex number to the fourth
power.
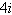
a. | 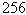 | b. | –64 | c. | 64 | d. | 16 | e. |  |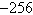
|
|
|
14.
|
Find all solutions to the equation  .
|
|
|
15.
|
Determine whether  is a solution
of the inequality  .
|
|
|
16.
|
Solve the inequality.
|
|
|
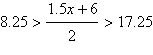
17.
|
Use absolute value notation to define the interval
(or pair of intervals) on the real number line.
All real numbers more than 
units from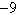 
|
|
|
18.
|
Determine whether the value of 
is a solution of the inequality.
|
|
|
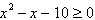
19.
|
Use a graphing utility to graph the equation. Use
the graph to approximate the values of  that satisfy the
inequality.
Equation: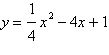
Inequalities:
|
|
|
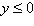
20.
|
Solve the inequality and graph the solution on the
real number line.
|
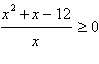