Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The given points represent the vertices of a
triangle.Select the triangle ABC in the coordinate plane.
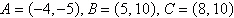
|
|
|
2.
|
A moving conveyor is built so that it rises 5 meter
for each 7 meters of horizontal travel. The conveyor runs between two floors in a factory. The
distance between the floors is 4 meters. Find the length of the conveyor. Round your answers to one
decimal place.
|
|
|
3.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
Vertical axis and passes
through the point 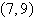
|
|
|
4.
|
The revenue R (in dollars) generated by the
sale of x units of a digital camera is given by
 . .
Approximate the number
of sales that will maximize revenue.
a. | Maximum revenue occurs at  units.
units. | b. | Maximum revenue occurs at  units.
units. | c. | Maximum revenue occurs at  units.
units. | d. | Maximum revenue occurs at  units.
units. | e. | Maximum revenue occurs at  units.
units. |
|
|
|
5.
|
Find the vertex and focus of the parabola.
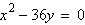
a. | vertex: (0, 0) focus: 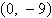 | b. | vertex: (0,
0) focus: 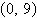 | c. | vertex:  focus: (0,
0) focus: (0,
0) | d. | vertex:  focus: (0,
0) focus: (0,
0) | e. | vertex: (0, 0) focus: 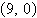 |
|
|
|
6.
|
Select the graph for following
equation.
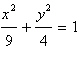
|
|
|
7.
|
Find the standard form
of the equation of the ellipse with the given characteristics and center at the
origin.
Foci:  ; major axis of length ; major axis of length 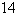
|
|
|
8.
|
Find the center and the vertices of the
ellipse.
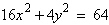
a. | center: (–8,
8) vertices: (–2, –4), (2,
4) | b. | center: (0,
0) vertices: (0, –4), (0,
4) | c. | center: (0,
0) vertices: (–4, –2), (4,
2) | d. | center: (0,
0) vertices: (–4, 0), (4,
0) | e. | center: (–8,
8) vertices: (–2, 0), (2,
0) |
|
|
|
9.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
vertices:  foci: foci: 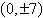
|
|
|
10.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
foci:  asymptotes: asymptotes: 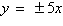
|
|
|
11.
|
Select the curve represented by the parametric
equations.
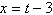
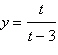
|
|
|
12.
|
Select the curve represented by the parametric
equations.
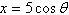
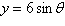
|
|
|
13.
|
Using following result find a set of parametric
equation of conic.
Circle:  , , 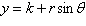
Circle: center:  ; radius: ; radius: 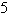
|
|
|
14.
|
A projectile is launched at a height of h
feet above the ground at an angle of  with the horizontal. The initial velocity is with the horizontal. The initial velocity is
 feet per second, and the path of the
projectile is modeled by the parametric equations feet per second, and the path of the
projectile is modeled by the parametric equations
 and and  . .
Select the correct graph of the path of a projectile launched from ground level at
the value of  and and  . .
 , ,  feet per second feet per second
|
|
|
15.
|
A point in rectangular coordinates is given.
Convert the point to polar coordinates.
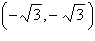
|
|
|
16.
|
Use a graphing utility to find one set of polar
coordinates for the point given in rectangular coordinates. Round your answers to three decimal
places.
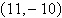
|
|
|
17.
|
Select the correct graph of the polar equation.
Describe your viewing window.
 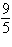
|
|
|
18.
|
Identify the conic and select its correct
graph.
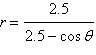
|
|
|
19.
|
Select the polar equation with graph.
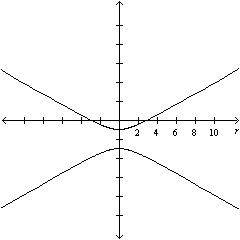
|
|
|
20.
|
Find a polar equation of the conic with its focus
at the pole.
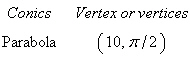
|