Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Find the slope of the line with inclination  . Round your answer to four decimal places. . Round your answer to four decimal places.
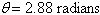
|
|
|
2.
|
Find the angle  (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree. (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree.
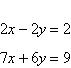
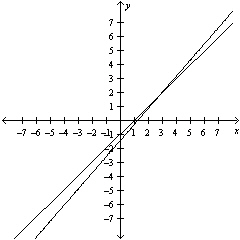
|
|
|
3.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
directrix: x =
1
a. | x2 =
y | b. | y2 =
–4x | c. | x2 = 4y | d. | x2 = –4y | e. | y2 = x |
|
|
|
4.
|
Find the vertex and focus of the parabola.
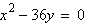
a. | vertex: (0, 0) focus: 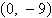 | b. | vertex: (0,
0) focus: 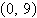 | c. | vertex:  focus: (0,
0) focus: (0,
0) | d. | vertex:  focus:
(0, 0) focus:
(0, 0) | e. | vertex: (0, 0) focus: 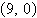 |
|
|
|
5.
|
Give the standard form of the equation of the
parabola with the given characteristics.
vertex: (–1,
–3) directrix: 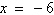
|
|
|
6.
|
A solar oven uses a parabolic reflector to focus
the sun's rays at a point 6 inches from the vertex of the reflector (see figure). Write an
equation for a cross section of the oven's reflector with its focus on the positive y
axis and its vertex at the origin.
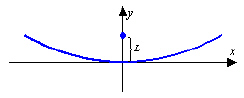
L = 6 inches
|
|
|
7.
|
Identify the conic as a
circle or an ellipse then find the center.
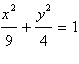
a. | Circle
Center: 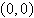 | b. | Ellipse
Center:
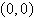 |
|
|
|
8.
|
Find the standard form of the equation of the
ellipse with the following characteristics.
foci:  major axis of length:
12 major axis of length:
12
|
|
|
9.
|
Use a graphing utility
to graph the conic. Determine the angle  through which the axes are
rotated. through which the axes are
rotated.
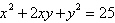
|
|
|
10.
|
Use the discriminant to
classify the graph.
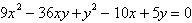
a. | The graph is a cone. | b. | The graph is a circle. | c. | The graph is a
parabola. | d. | The graph is a ellipse. | e. | The graph is a hyperbola. |
|
|
|
11.
|
Use the Quadratic
Formula to solve for  . .
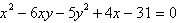
|
|
|
12.
|
Consider the
equation.
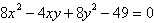
Without
calculating, explain how to rewrite the equation so that it does not have an  -term. -term.
|
|
|
13.
|
Eliminate the parameter and write the corresponding
rectangular equation whose graph represents the curve.
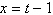
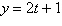
|
|
|
14.
|
Eliminate the parameter and write the corresponding
rectangular equation whose graph represents the curve.
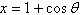
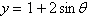
|
|
|
15.
|
A projectile is launched at a height of h
feet above the ground at an angle of  with the horizontal. The initial velocity is with the horizontal. The initial velocity is
 feet per second, and the path of the
projectile is modeled by the parametric equations feet per second, and the path of the
projectile is modeled by the parametric equations
 and and  . .
Select the correct graph of the path of a projectile launched from ground level at
the value of  and and  . .
 , ,  feet per second feet per second
|
|
|
16.
|
A point in rectangular coordinates is given.
Convert the point to polar coordinates.
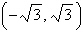
|
|
|
17.
|
Convert the polar equation to rectangular
form.
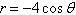
|
|
|
18.
|
Select the graph of  over the
interval. Describe the part of the graph obtained in this case. over the
interval. Describe the part of the graph obtained in this case.
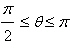
a. |
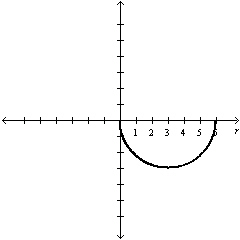
Lower half of
circle | d. |
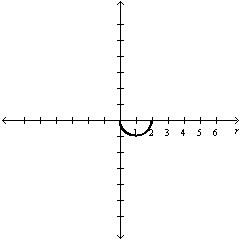
Lower half of
circle | b. |
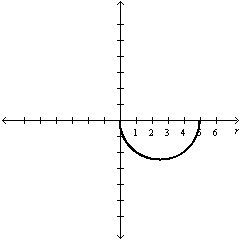
Lower half of
circle | e. |
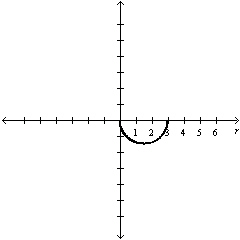
Lower half of
circle | c. |
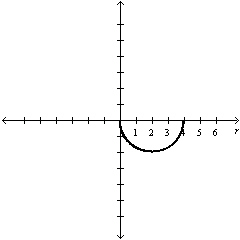
Lower half of
circle |
|
|
|
19.
|
Select the polar equation of the conic for  and identify the conic for the following equation. and identify the conic for the following equation.
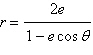
|
|
|
20.
|
By using a graphing utility select the correct
graph of the polar equation.
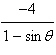
|