Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Use fundamental identities to simplify the
expression below and then determine which of the following is not equivalent.
|
|
|
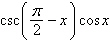
2.
|
Factor; then use fundamental identities to simplify
the expression below and determine which of the following is not equivalent.
|
|
|
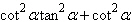
3.
|
Factor; then use fundamental identities to simplify
the expression below and determine which of the following is not equivalent.
|
|
|
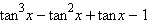
4.
|
Which of the following is equivalent to the given
expression?
|
|
|
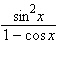
5.
|
If  , use trigonometric
substitution to write  as a trigonometric function of q, where  .
|
|
|
6.
|
Solve the following equation.
|
|
|
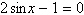
7.
|
Solve the following equation.
|
|
|
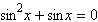
8.
|
Solve the following equation.
|
|
|
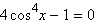
9.
|
Solve the multiple-angle equation.
|
|
|
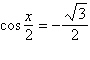
10.
|
Use the Quadratic Formula to solve the given
equation on the interval  ; then use a graphing utility to approximate
the angle x. Round answers to three decimal places.
|
|
|
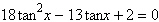
11.
|
Use inverse functions where needed to find all
solutions (if they exist) of the given equation on the interval  .
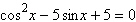
a. | 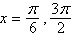 | b. | 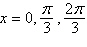 | c. | 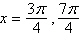 | d. | 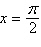 | e. | solution does not exist |
|
|
|
12.
|
Find the exact value of the given
expression.
|
|
|
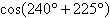
13.
|
Find the exact value of the given expression using
a sum or difference formula.
|
|
|
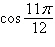
14.
|
Find the exact value of the given expression using
a sum or difference formula.
|
|
|
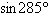
15.
|
Write the given expression as the sine of an
angle.
|
|
|
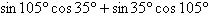
16.
|
Find the exact value of  given that
 and  . (Both
u and v are in Quadrant II.)
|
|
|
17.
|
Find the exact value of  given that
 and  . (Both
u and v are in Quadrant II.)
|
|
|
18.
|
Find the exact solutions of the given equation in
the interval  .
|
|
|
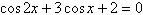
19.
|
Use a double-angle formula to find the exact value
of  when  .
|
|
|
20.
|
Use the figure below to find the exact value of the
given trigonometric expression.
|
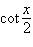
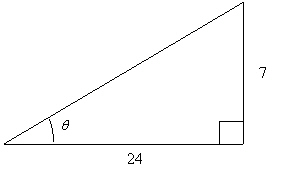