Name: 
 

Chapter 3 Pre Test


Multiple Choice
Identify the choice that best completes the statement or answers the question.
 

 1. 
Evaluate the function mc001-1.jpg at mc001-2.jpg. Round to 3 decimal places.
a.
5.287
b.
2.572
c.
4.680
d.
1.690
e.
20.055
 

 2. 
What is the value of the function mc002-1.jpg at mc002-2.jpg? Round to 3 decimal places.
a.
1.398
b.
0.676
c.
1.795
d.
–7.747
e.
0.848
 

 3. 
What is the value of the function mc003-1.jpg at mc003-2.jpg? Round to 3 decimal places.
a.
26.492
b.
37.296
c.
42.051
d.
7.597
e.
82.783
 

 4. 
Use the One-to-One Property to solve the following equation for x.
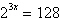
mc004-1.jpg
a.
mc004-2.jpg
b.
mc004-3.jpg
c.
mc004-4.jpg
d.
mc004-5.jpg
e.
2
 

 5. 
Use the One-to-One Property to solve the following equation for x.
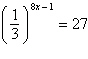
mc005-1.jpg
a.
mc005-2.jpg
b.
mc005-3.jpg
c.
mc005-4.jpg
d.
mc005-5.jpg
e.
mc005-6.jpg
 

 6. 
Rewrite the logarithmic equation mc006-1.jpg in exponential form.
a.
mc006-2.jpg
b.
mc006-3.jpg
c.
mc006-4.jpg
d.
mc006-5.jpg
e.
mc006-6.jpg
 

 7. 
Evaluate the function mc007-1.jpg at mc007-2.jpg without using a calculator.
a.
–2
b.
–3
c.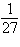
mc007-3.jpg
d.
27
e.
–4
 

 8. 
Identify the value of the function mc008-1.jpg at mc008-2.jpg. Round to 3 decimal places.
a.
3.118
b.
4.118
c.
2.618
d.
6.028
e.
3.618
 

 9. 
Write the exponential equation mc009-1.jpg in logarithmic form.
a.
mc009-2.jpg
b.
mc009-3.jpg
c.
mc009-4.jpg
d.
mc009-5.jpg
e.
mc009-6.jpg
 

 10. 
Identify the x-intercept of the function mc010-1.jpg.
a.
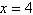mc010-2.jpg
b.
The function has no x-intercept.
c.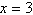
mc010-3.jpg
d.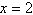
mc010-4.jpg
e.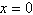
mc010-5.jpg
 

 11. 
Rewrite the logarithm mc011-1.jpg in terms of the common logarithm (base 10).
a.
mc011-2.jpg
b.
mc011-3.jpg
c.
mc011-4.jpg
d.
mc011-5.jpg
e.
mc011-6.jpg
 

 12. 
Rewrite the logarithm mc012-1.jpg in terms of the natural logarithm.
a.
mc012-2.jpg
b.
mc012-3.jpg
c.
mc012-4.jpg
d.
mc012-5.jpg
e.
mc012-6.jpg
 

 13. 
Evaluate the logarithm mc013-1.jpg using the change of base formula. Round to 3 decimal places.
a.
0.630
b.
0.273
c.
–0.692
d.
–1.745
e.
–0.573
 

 14. 
Find the exact value of mc014-1.jpg without using a calculator.
a.
mc014-2.jpg
b.
–1
c.
mc014-3.jpg
d.
mc014-4.jpg
e.
mc014-5.jpg
 

 15. 
Simplify the expression mc015-1.jpg.
a.
1
b.
The expression cannot be simplified.
c.
–108
d.
–12
e.
4
 

 16. 
Put the expressions in the appropriate order: mc016-1.jpg.
a.
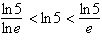mc016-2.jpg
b.
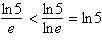mc016-3.jpg
c.
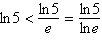mc016-4.jpg
d.
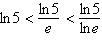mc016-5.jpg
e.
The expressions are equivalent.
 

 17. 
Solve for x: mc017-1.jpg. Round to 3 decimal places.
a.
13.291
b.
10.518
c.
–3.794
d.
–13.291
e.
7.587
 

 18. 
Solve for x: mc018-1.jpg. Round to 3 decimal places.
a.
2.407
b.
–1.362
c.
0.407
d.
1.362
e.
no solution
 

 19. 
An initial investment of $9000 grows at an annual interest rate of 5% compounded continuously. How long will it take to double the investment?
a.
1 year
b.
13.86 years
c.
14.86 years
d.
13.40 years
e.
14.40 years
 

 20. 
The population P of a bacteria culture is modeled by mc020-1.jpg, where t is the time in hours. If the population of the culture was 5800 after 40 hours, how long does it take for the population to double? Round to the nearest tenth of an hour.
a.
59.3 hours
b.
94.5 hours
c.
9.6 hours
d.
57.5 hours
e.
92.7 hours
 



 
Check Your Work     Start Over