Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Find the coordinates of
the point.
The point is located six units behind the  -plane,
seven units to the right of the  -plane, and
eight units above the  -plane.
a. |   ,  ,  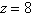| b. |   ,  ,  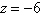| c. |   ,  ,  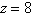| d. |   ,  ,  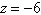| e. |  6,  ,  |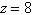
|
|
|
2.
|
Find the distance
between the points.
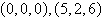
a. | 
units | b. | 
units | c. |  units | d. |  units | e. |  units |
|
|
|
3.
|
Find the distance
between the points.
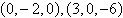
a. | 
units | b. | 
units | c. | 
units | d. | 
units | e. | 
units |
|
|
|
4.
|
Determine the octant(s) in which
(x,y,z) is located so that the conditions are satisfied.
x > 0, y > 0, z > 0
a. | octant V | b. | octant I | c. | octant
III | d. | octant I or octant II | e. | octant VIII |
|
|
|
5.
|
Find the midpoint of the line segment joining the
points.
(4, 6, 4), (–9, 9, –1)
|
|
|
6.
|
Find the standard form of the equation of the
sphere with the given characteristics.
Center: (9, 8,
–9); radius 9
|
|
|
7.
|
Find the vector z, given  .
|
|
|
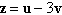
8.
|
Find the dot product of u and
v.
|
|
|
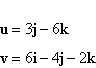
9.
|
Use vectors to determine whether the points are
collinear.
(9, –7, –6), (5, –9, –7),
(13, –5, –5)
a. | collinear | b. | not collinear |
|
|
|
10.
|
Use vectors to determine whether the points are
collinear.
(7, 5, –3), (2, 3, –4), (3, 2,
–5)
a. | not collinear | b. | collinear |
|
|
|
11.
|
Use the vectors u and v to find  .
|
|
|
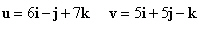
12.
|
Find  and show that it is
orthogonal to both u and v.
|
|
|
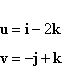
13.
|
Find the area of the parallelogram that has the
vectors as adjacent sides.
|
|
|
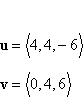
14.
|
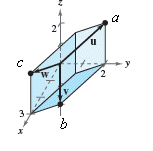
Use the triple scalar product to find the volume of
the parallelepiped having adjacent edges u,v, and w.
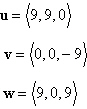
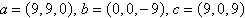
a. |  cubic
units | b. |  cubic
units | c. |  cubic
units | d. |  cubic
units | e. |  cubic
units |
|
|
|
15.
|
Find u ´
v.
u = 4i + j –
3k, v = –3i + 5j + k
a. | –10 | b. | –12i + 5j – 3k | c. | 16i – 5j + 23k | d. | –20 | e. | 16i +
5j + 23k |
|
|
|
16.
|
Find the area of the triangle with the given
vertices.
(5, –1, 2), (7,–4,–2), (2,
–6, 3)
|
|
|
17.
|
Find the general form of the equation of the plane
passing through the point and perpendicular to the specified vector or line.
Point: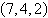 
Perpendicular to: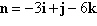 
|
|
|
18.
|
Find a set of symmetric equations of the line that
passes through the given points.
|
|
|
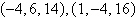
19.
|
Find a set of parametric equations of the
line.
Passes through  and is parallel to the xy-plane and
the yz-plane
|
|
|
20.
|
Find the general form of the equation of the plane
passing through the point and perpendicular to the specified line. [Be sure to reduce the
coefficients in your answer to lowest terms by dividing out any common factor.]
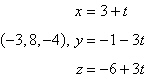
a. | 3x – 8y + 4z + 39 =
0 | b. | 3x – 8y + 4z – 39 =
0 | c. | x – 3y + 3z – 39 =
0 | d. | x – 3y + 3z + 39 =
0 | e. | x – 3y + 3z =
0 |
|