|
|
|
1.
|
Select the augmented matrix for the system of
linear equations.
|
|
|
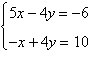
2.
|
Fill in the blank(s) using elementary row
operations to form a row-equivalent matrix.
|
|
|
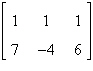
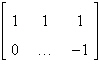
3.
|
Write the augmented matrix for the system of linear
equations.
|
|
|
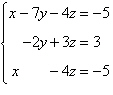
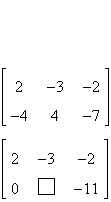
4.
|
Fill in the blank using elementary row operations
to form a row-equivalent matrix.
|
|
|
5.
|
Determine whether the two systems of linear
equations yield the same solutions. If so, find the solutions using matrices.
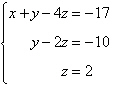
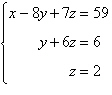
a. | x = –3, y = –6, z =
2 | b. | The systems yield different
solutions. | c. | x = 3,
y = 2, z = –3 | d. | x = 3,
y = 6, z = 2 | e. | x =
–6, y = 2, z = –3 |
|
|
|
6.
|
Find  .
|
|
|
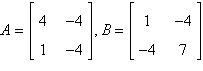
7.
|
Evaluate the expression.
|
|
|
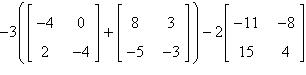
8.
|
Evaluate the expression.
|
|
|
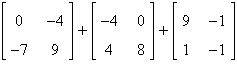
9.
|
Solve for X in the equation given.
|
|
|
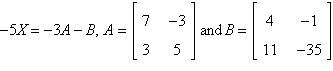
10.
|
Find the inverse of the matrix  .
|
|
|
11.
|
Find the inverse of the matrix 
(if it exists).
|
|
|
12.
|
Use the matrix capabilities of a graphing utility
to solve the following system of linear equations:
|
|
|
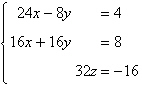
13.
|
Find all the cofactors of the
matrix.
|
|
|
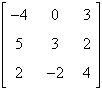
14.
|
Find the determinant of the matrix by the method of
expansion by cofactors. Expand using the column 2.
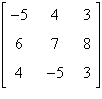
a. | –423 | b. | 423 | c. | –421 | d. | –422 | e. | –424 |
|
|
|
15.
|
Find  .
|
|
|
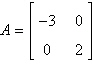
16.
|
Use the matrix capabilities of a graphing utility
to find the determinant of the matrix
 .
|
|
|
17.
|
Use a graphing utility and Cramer’s Rule to
solve (if possible) the system of equations.
|
|
|
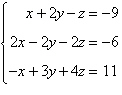
18.
|
Use Crammer’s Rule to solve (if possible) the
system of equations.
|
|
|
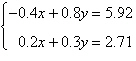
19.
|
Find a value of such that the triangle with the
given vertices has an area of 4 square units.
|
|
|
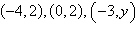
20.
|
Use a determinant to determine whether the points
 and  are
collinear.
a. |  ; therefore, the points are
not collinear. | b. |  ;
therefore, the points are collinear. |
|