|
|
|
1.
|
Find the sales necessary to break even 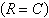 for the cost C of producing x units and the revenue R obtained by
selling x units. (Round to the nearest whole unit.) for the cost C of producing x units and the revenue R obtained by
selling x units. (Round to the nearest whole unit.)
a. | 100 units | b. | 300 units | c. | 0
unit | d. | 400 units | e. | 200 units |
|
|
|
2.
|
A small software company invests  to produce a software package that will sell for
to produce a software package that will sell for 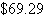 . Each unit can be produced
for . Each unit can be produced
for 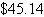 . How many units must be sold to break
even? . How many units must be sold to break
even?
a. | 905 units | b. | 805 units | c. | 1205
units | d. | 1005 units | e. | 1105 units |
|
|
|
3.
|
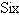 hundred gallons of hundred gallons of 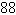 -octane gasoline is obtained by mixing -octane gasoline is obtained by mixing 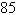 -octane gasoline with -octane gasoline with
 -octane gasoline. How much of each type of gasoline is required to obtain the -octane gasoline. How much of each type of gasoline is required to obtain the  gallons of gallons of 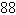 -octane gasoline? -octane gasoline?
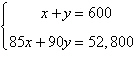
|
|
|
4.
|
Solve the system by the method of elimination and
check any solutions algebraically.
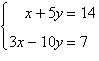
|
|
|
5.
|
Solve the system by the method of elimination and
check any solutions algebraically.
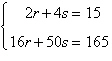
|
|
|
6.
|
Solve using any method.
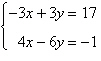
|
|
|
7.
|
During one performance of a local arts
council's presentation of Fiddler on the Roof, the box office sold 200 tickets and
collected $1372. If adult tickets sold for $8 and children's tickets sold for $6, how many of
each type of ticket were sold?
a. | adult tickets sold = 86; children's tickets sold =
114 | b. | adult tickets sold = 97; children's tickets sold =
125 | c. | adult tickets sold = 114; children's tickets sold =
86 | d. | adult tickets sold = 97; children's tickets sold =
99 | e. | adult tickets sold = 125; children's tickets sold =
97 |
|
|
|
8.
|
Find the equation of the parabola  that passes through the points.
that passes through the points.
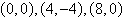
|
|
|
9.
|
The perimeter of a
triangle is 130 feet. The longest side of the triangle is 24 feet longer than the
shortest side. The sum of the lengths of the two shorter sides is 18 feet more than the length of the
longest side. Find the lengths of the sides of the triangle.
a. | 57 ft, 42 ft, 32 ft | b. | 56 ft, 43 ft, 32 ft | c. | 56 ft, 42 ft, 57
ft | d. | 56 ft, 42 ft, 32 ft | e. | 56 ft, 44 ft, 32 ft |
|
|
|
10.
|
You work as a disc jockey at your college radio
station. You are supposed to play 48 songs within two hours. You are to choose the songs from
the latest rock, dance, and pop albums. You want to play twice as many rock songs as pop songs and
four more pop songs
than dance songs. How many of each type of song will you
play?
a. | Rock =26
Dance = 9
Pop
=9 | b. | Rock =26
Dance = 9
Pop
=13 | c. | Rock =13
Dance = 9
Pop =
26 | d. | Rock =13
Dance = 9
Pop
=13 | e. | Rock =26
Dance = 13
Pop
=13 |
|
|
|
11.
|
In a particular area of the United States, the
electric utility company has determined that the average monthly electric bill (in dollars) for
homeowners varies with the average monthly temperature (degrees Fahrenheit) as shown in the table
below.
Average monthly
temp.
°F | Average monthly electric
bill
$ | 40 | 78 | 60 | 61 | 80 | 108 | | |
Find a least squares regression parabola that models the data and use that to
estimate the average monthly electric bill in a month with average temperature of
71 oF.
a. | y = 0.07(71)2 – 7.85(71) + 304 =
$100 | b. | y = 0.06(71)2 – 6.85(71) + 304 =
$120 | c. | y = 0.07(71)2 – 5.85(71) + 304 =
$242 | d. | y = 0.08(71)2 – 8.85(71) + 304 =
$79 | e. | y = 0.08(71)2 – 4.85(71) + 304 =
$363 |
|
|
|
12.
|
Write the form of the partial fraction
decomposition of the rational expression. Do not solve for the constants.
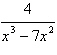
|
|
|
13.
|
Write the partial fraction decomposition of the
rational expression. Check your result algebraically.
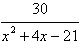
|
|
|
14.
|
Write the partial fraction decomposition of the
rational expression. Check your result algebraically.
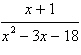
|
|
|
15.
|
Write the partial fraction decomposition of the
rational expression.
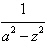
|
|
|
16.
|
Select an inequality for the shaded region shown in
the figure.
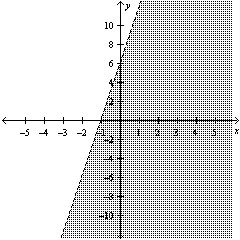
|
|
|
17.
|
Select a set of inequalities to describe the
region.
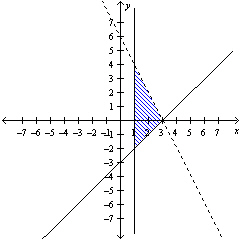
|
|
|
18.
|
A small company that manufactures two models of
exercise machines has an order for 14 units of the standard model and 15 units of the deluxe model.
The company has trucks of two different sizes that can haul the products, as shown in the
table.
Truck | Standard | Deluxe | Large | 6 | 3 | Medium | 4 | 6 | | | |
Find and graph a system of inequalities describing the numbers of trucks
of each size that are needed to deliver the order.
|
|
|
19.
|
Sketch the graph of the inequality.
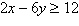
|
|
|
20.
|
A manufacturer produces two models of elliptical
cross-training exercise machines.
The times for assembling, finishing, and packaging model X are 3
hours, 3 hours, and 0.8 hour, respectively. The times for model Y are 4 hours, 2.5 hours, and 0.4
hour. The total times available for assembling, finishing, and packaging are 6000 hours, 4200 hours,
and 950 hours, respectively. The profits per unit are 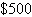 for model X and for model X and 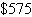 for model Y. What is the optimal production level for each model? What is the optimal
profit? for model Y. What is the optimal production level for each model? What is the optimal
profit?
a. | 6000 units of model X
950 units of model Y
Optimal
profit: 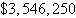 | b. | 950 units of model X
6000 units of model Y
Optimal profit: 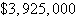 | c. | 400 units of model
X
1200 units of model Y
Optimal profit: 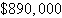 | d. | 950 units of model X
4200 units of model Y
Optimal profit: 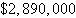 | e. | 4200 units of
model X
950 units of model Y
Optimal profit: 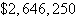 |
|