|
|
|
1.
|
The weekly rentals for a newly released DVD of an
animated film at a local video store decreased each week. At the same time, the weekly rentals for a
newly released DVD of a horror film increased each week. Models that approximate the weekly rentals
R for each DVD are
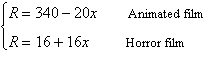
where x represents the number
of weeks each DVD was in the store, with 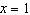 corresponding to the first week. After how
many weeks will the rentals for the two movies be equal?
a. | 11 weeks | b. | 7 weeks | c. | 5
weeks | d. | 13 weeks | e. | 9 weeks |
|
|
|
2.
|
Solve the system by the method of
substitution.
|
|
|
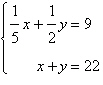
3.
|
Solve the system by the method of
substitution.
|
|
|
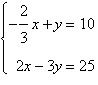
4.
|
Solve the system by the method of elimination and
check any solutions algebraically.
|
|
|
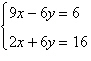
5.
|
Find the equilibrium point of the demand and supply
equations. The equilibrium point is the price p and number of units x that satisfy both
the demand and supply equations.
|
|
|
6.
|
Find the equilibrium point of the demand and supply
equations. The equilibrium point is the price p and number of units x that satisfy both
the demand and supply equations.
|
|
|
7.
|
Solve the system by the method of elimination and
check any solutions algebraically.
|
|
|
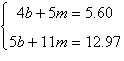
8.
|
Solve the system of linear equations and check any
solution algebraically.
|
|
|
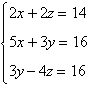
9.
|
Perform the row operation and find the equivalent
system.
Add Equation 1 to Equation 2.
|
|
|
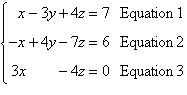
10.
|
Write the form of the partial fraction
decomposition of the rational expression. Do not solve for the constants.
|
|
|
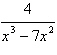
11.
|
Write the partial fraction decomposition of the
rational expression.
|
|
|
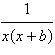
12.
|
Write the partial fraction decomposition of the
rational expression.
|
|
|
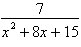
13.
|
Select a set of inequalities to describe the
region.
|
|
|
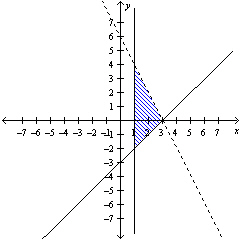
14.
|
Find the consumer surplus and producer
surplus.
Demand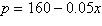 
Supply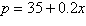 
|
|
|
15.
|
A dietitian is asked to design a special dietary
supplement using two different foods. Each ounce of food X contains 20 units of calcium, 15 units of
iron, and 10 units of vitamin B. Each ounce of food Y contains 10 units of calcium, 10 units of iron,
and 20 units of vitamin B. The minimum daily requirements of the diet are 200 units of calcium, 150
units of iron, and 250 units of vitamin B. Write a system of inequalities describing the different
amounts of food X and food Y that can be used.
|
|
|
16.
|
Find the maximum value of the objective function
and where it occurs, subject to the indicated constraints.
Objective function:
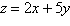
Constraints:
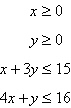
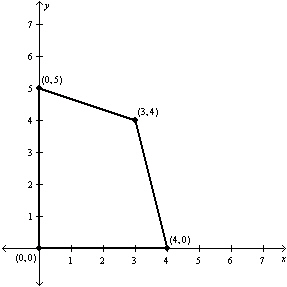
a. | Maximum at 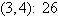 | b. | Maximum at 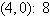 | c. | Maximum at 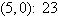 | d. | Maximum at 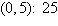 | e. | Maximum at  |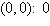
|
|
|
17.
|
Find the minimum value of the objective function
and where it occurs, subject to the indicated constraints.
Objective function:
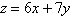
Constraints:
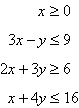
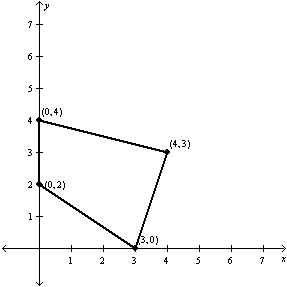
a. | Minimum at 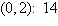 | b. | Minimum at 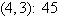 | c. | Minimum at 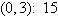 | d. | Minimum at 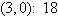 | e. | Minimum at  |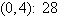
|
|
|
18.
|
Select the region determined by the constraints.
Then find the maximum value of the objective function (if possible) and where it occurs, subject to
the indicated constraints.
Objective function:
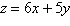
Constraints:
|
|
|
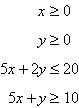
19.
|
The linear programming problem has an unusual
characteristic. Select a graph of the solution region for the problem and describe the unusual
characteristic. Find the minimum value of the objective function (if possible) and where it
occurs.
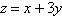
Constraints:
|
|
|
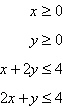
20.
|
An accounting firm has 780 hours of staff time and
272 hours of reviewing time
available each week. The firm charges  for an audit
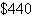and  for a tax return. Each audit requires 60
hours of staff time and 16 hours of review time. Each tax return requires 10 hours of staff time and
4 hours of review time. What numbers of audits and tax returns will yield an optimal revenue? What is
the optimal revenue?
a. | 0 audit
65 tax returns
Optimal revenue: 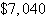 | b. | 5 audits
48 tax
return
Optimal revenue: 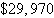 | c. | 16 audits
0 tax return
Optimal revenue: 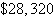 | d. | 10 audits
10
tax returns
Optimal revenue: 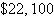 | e. | 13 audit
0 tax returns
Optimal revenue:  |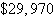
|