|
|
|
1.
|
Use the Law of Sines to
solve (if possible) the triangle. Round your answers to two decimal places.
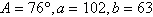
|
|
|
2.
|
In the figure,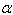 and and 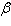 are positive angles. are positive angles.
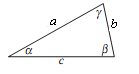
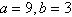
Write 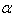 as a function of as a function of 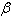 . .
|
|
|
3.
|
A park ranger at point A observes a fire in
the direction  . Another ranger at point B, 5 miles due
east of A, sites the same fire at . Another ranger at point B, 5 miles due
east of A, sites the same fire at 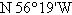 . Determine the distance from point B to
the fire. Round answer to two decimal places. . Determine the distance from point B to
the fire. Round answer to two decimal places.
a. | 2.18 miles | b. | 4.55 miles | c. | 2.51
miles | d. | 4.84 miles | e. | 4.20 miles |
|
|
|
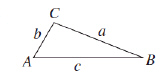
4.
|
Use the law of Cosines to solve the given triangle.
Round your answer to two decimal places.
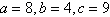
|
|
|
5.
|
Use the law of Cosines to solve the given triangle.
Round your answer to two decimal places.
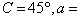 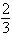 , b = , b =
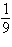
|
|
|
6.
|
Determine the angle 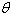 in the design
of the streetlight shown in the following figure. in the design
of the streetlight shown in the following figure.
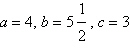 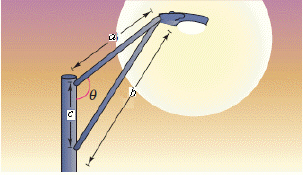
|
|
|
7.
|
Given  , , 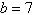 , and , and 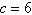 , use the Law of Cosines to solve the triangle for the value of C. Round your
answer to two decimal places. , use the Law of Cosines to solve the triangle for the value of C. Round your
answer to two decimal places.
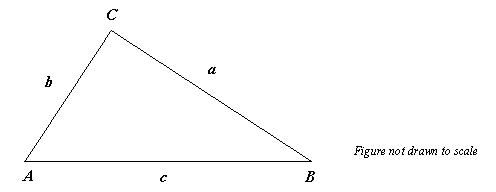
|
|
|
8.
|
Given 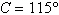 , , 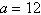 , and , and 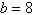 , use the Law of Cosines to solve the triangle for the value of c. Round your
answer to two decimal places. , use the Law of Cosines to solve the triangle for the value of c. Round your
answer to two decimal places.
a. | 16.29 | b. | 11.26 | c. | 15.57 | d. | 17.00 | e. | 14.13 |
|
|
|
9.
|
A vertical pole 29 feet tall stands on a hillside
that makes an angle of 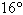 with the horizontal. Determine the approximate
length of cable that would be needed to reach from the top of the pole to a point 78 feet downhill
from the base of the pole. Round your answer to two decimal places. with the horizontal. Determine the approximate
length of cable that would be needed to reach from the top of the pole to a point 78 feet downhill
from the base of the pole. Round your answer to two decimal places.
a. | 82.88 feet | b. | 75.35 feet | c. | 99.45
feet | d. | 88.40 feet | e. | 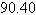 feet feet |
|
|
|
10.
|
Select a linear combination of the standard unit
vectors i and j of given initial and terminal points of a vector.
Initial Point | Terminal Point | | | | |
|
|
|
11.
|
|
|
|
12.
|
Find a unit vector in the direction of 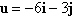 . .
|
|
|
13.
|
|
|
|
14.
|
Given vectors 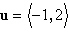 and and 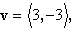 determine the quantity indicated below. determine the quantity indicated below.
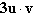
|
|
|
15.
|
A 725-pound trailer is sitting on an exit ramp
inclined at 36° on Highway 35. How much force is required to keep the trailer from rolling back
down the exit ramp? Round your answer to two decimal places.
a. | 566.49 pounds | b. | 546.44 pounds | c. | 586.54
pounds | d. | 506.34 pounds | e. | 426.14 pounds |
|
|
|
16.
|
Plot the complex number
and find its absolute value.
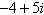
|
|
|
17.
|
Find the standard form
of the complex number. Then represent the complex number graphically.
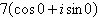
|
|
|
18.
|
Find the trigonometric form of the complex number
shown below.
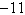
|
|
|
19.
|
Find the product 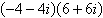 using
trigonometric forms. Leave the result in trigonometric form. using
trigonometric forms. Leave the result in trigonometric form.
|
|
|
20.
|
Find the fifth roots of  Write the
roots in trigonometric form. Write the
roots in trigonometric form.
|