|
|
|
1.
|
Use the Law of Sines to
solve (if possible) for 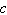 . Round your answers to two decimal
places. . Round your answers to two decimal
places.
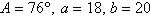
|
|
|
2.
|
Use the Law of Sines to
solve (if possible) for  . Round your answers to two decimal
places. . Round your answers to two decimal
places.
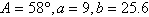
|
|
|
3.
|
Find values for 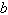 such that
the triangle has one solution. such that
the triangle has one solution.
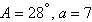
|
|
|
4.
|
Determine a value for b such that a triangle
with  and and 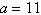 has only one
solution. has only one
solution.
|
|
|
5.
|
Use the law of Cosines to solve the given triangle.
Round your answer to two decimal places.
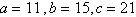
|
|
|
6.
|
Use the law of Cosines to solve the given triangle.
Round your answer to two decimal places.
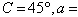 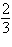 , b = , b =
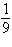
|
|
|
7.
|
Find 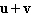 . .
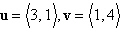
|
|
|
8.
|
Find a unit vector in the direction of the given
vector.
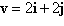
|
|
|
9.
|
Find a unit vector in the direction of 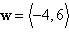 . .
|
|
|
10.
|
Let w be a vector with initial point 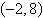 and terminal point and terminal point  . Write w as a linear combination of
the standard unit vectors i and j. . Write w as a linear combination of
the standard unit vectors i and j.
|
|
|
11.
|
Find the component form of v if  and the angle it makes with the x-axis is and the angle it makes with the x-axis is 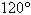 . .
|
|
|
12.
|
Find the dot product of u and
v.
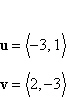
|
|
|
13.
|
Use the vector 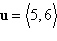 to find
the indicated quantity. State whether the result is a vector or a scalar. to find
the indicated quantity. State whether the result is a vector or a scalar.
a. | 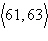 ;
vector ;
vector | b. | 63; scalar | c. | 61; scalar | d. | 59;
scalar | e. | 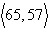 ;
vector ;
vector |
|
|
|
14.
|
Use the dot product to find the magnitude of
u.
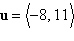
|
|
|
15.
|
Find the trigonometric form of the complex number
shown below.
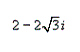
|
|
|
16.
|
Find the standard form of the complex number  . Round values to the nearest hundredth. . Round values to the nearest hundredth.
|
|
|
17.
|
Divide the complex numbers below and leave the
result in trigonometric form.
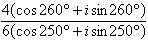
|
|
|
18.
|
Find the product  using
trigonometric forms. Leave the result in trigonometric form. using
trigonometric forms. Leave the result in trigonometric form.
|
|
|
19.
|
Use DeMoivre's Theorem to find the indicated
power of the following complex number.
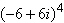
a. | 5,184 | b. | 7,776 | c. | 46,656 | d. | 186,624 | e. | –5,184 |
|
|
|
20.
|
Use DeMoivre's Theorem to find the indicated
power of the following complex number.
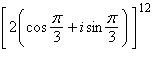
a. | 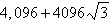 | b. | 2048 | c. | 4,096 | d. | –4,096 | e. | 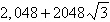 |
|