|
|
|
1.
|
Select the graph of the function. 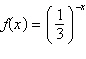
|
|
|
2.
|
Use a graphing utility to construct a table of values for the function. Round
your answer to three decimal places. 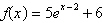
|
|
|
3.
|
Select the graph of the exponential function. 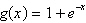
|
|
|
4.
|
Write the logarithmic equation in exponential form. 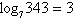
|
|
|
5.
|
Evaluate the function at the indicated value of 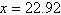 . Round your
result to three decimal places. 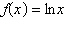 a. | 3.132 | b. | –2.033 | c. | –3.132 | d. | 2.033 | e. | 22.92 |
|
|
|
6.
|
Evaluate the function at the indicated value of 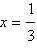 . Round your
result to three decimal places. 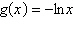 a. | –1.099 | b. | 3 | c. | 1.792 | d. | –1.792 | e. | 1.099 |
|
|
|
7.
|
Find the exact value of the logarithmic expression without using a
calculator. 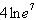
|
|
|
8.
|
Condense the expression to the logarithm of a single quantity. 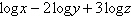
|
|
|
9.
|
Use the properties of logarithms to rewrite and simplify the logarithmic
expression. 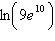
|
|
|
10.
|
Evaluate the logarithm 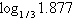 using the change of base
formula. Round to 3 decimal places. a. | –1.745 | b. | –0.692 | c. | 0.630 | d. | 0.273 | e. | –0.573 |
|
|
|
11.
|
Find the exact value of 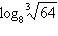 without using a
calculator.
|
|
|
12.
|
Find the exact value of 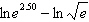 without using a
calculator.
|
|
|
13.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 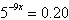
|
|
|
14.
|
Solve the exponential equation algebraically. Approximate the result to three
decimal places. 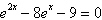
|
|
|
15.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 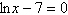
|
|
|
16.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 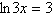
|
|
|
17.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 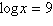 a. | 100,000,000 | b. | 100,000,000,000 | c. | 1,000,000,000 | d. | 10,000,000,000 | e. | 10,000,000 |
|
|
|
18.
|
Solve the logarithmic equation algebraically. Approximate the result to three
decimal places. 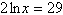
|
|
|
19.
|
Solve the equation algebraically. Round the result to three decimal places.
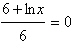
|
|
|
20.
|
The population P of a culture of bacteria is described by the equation
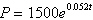 , where t is the time, in hours,
relative to the time at which the population was 1500. What was the population at 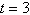 hours?
|