Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Select the graph of the quadratic function 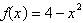 . Identify the vertex and axis of symmetry.
|
|
|
2.
|
Determine the vertex of the graph of the quadratic
function  .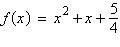
|
|
|
3.
|
Write the quadratic function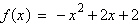 
in standard form.
|
|
|
4.
|
Find all the real zeros of the polynomial function
and determine the multiplicity of each zero and the number of turning points of the graph of the
function.
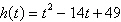
a. | All Real Zeros: 0,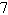 ; Even
multiplicity; number of turning points: 2 | b. | All Real Zeros:
 ; Even multiplicity; number of turning points:
1 | c. | All Real Zeros: 0,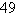 ; Odd
multiplicity; number of turning points: 2 | d. | All Real Zeros:
0,1, ; Even multiplicity; number of turning points:
3 | e. | All Real Zeros:  ; Odd
multiplicity; number of turning points: 1 |
|
|
|
5.
|
Select the graph of the function and use the zero
or root feature to approximate the real zeros of the function.
|
|
|
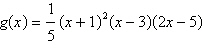
6.
|
Describe the right-hand and the left-hand behavior
of the graph of  .
a. | Because the degree is odd and the leading coefficient is
negative, the graph rises to the left and falls to the right. | b. | Because the degree is odd and the leading coefficient is negative, the graph
falls to the left and rises to the right. | c. | Because the degree
is odd and the leading coefficient is positive, the graph falls to the left and falls to the
right. | d. | Because the degree is odd and the leading coefficient is
positive, the graph rises to the left and rises to the right. | e. | Because the degree is even and the leading coefficient is negative, the graph
rises to the left and falls to the right. |
|
|
|
7.
|
Use the Remainder Theorem and synthetic division to
find the function value.
 
|
|
|
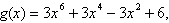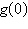
8.
|
The amounts A (in billions of dollars) donated to
support higher education in the United States from 2000 through 2007 are shown in the table, where
t represents the year, with  corresponding to 2000.
| Year, t | Amount, A | 0 | 23.3 | 1 | 24.3 | 2 | 24 | 3 | 24 | 4 | 24.5 | 5 | 25.7 | 6 | 28.1 | 7 | 29.9 | | |
Use a graphing
utility to select a correct a scatter plot of the above data.
|
|
|
9.
|
Use synthetic division to divide.
|
|
|
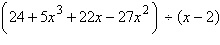
10.
|
Use the Remainder Theorem and synthetic division to
find the function value. Verify your
answer using another method.
 
|
|
|
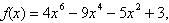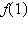
11.
|
Use synthetic division to divide.
|
|
|
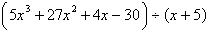
12.
|
Use the Remainder Theorem and synthetic division to
find each function value. Verify your
answers using another method.
 , 
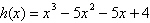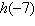
a. | –551 | b. | –545 | c. | –548 | d. | –549 | e. | –547 |
|
|
|
13.
|
Write the polynomial as the product of linear and
quadratic factors that are irreducible over the reals.
|
|
|
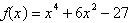
14.
|
Use the given zero to find all the zeros of the
function.
|
|
|
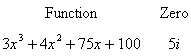
15.
|
Find all the zeros of the function and write the
polynomial as a product of linear factors.
|
|
|
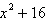
16.
|
State sales tax is based on retail price. An item
that sells for $197.99 has a sales tax of $11.4. Find a mathematical model that gives the amount of
sales tax y in terms of the retail price x. Use the model to find the sales tax on a
$639.99 purchase. (Round your answer to four decimal places.)
|
|
|
17.
|
Use the fact that the diameter of the largest
particle that can be moved by a stream varies approximately directly as the square of the velocity of
the stream.
A stream with a velocity of 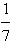 mile per hour can
move coarse sand particles about 0.03 inch in diameter. Approximate the velocity required to carry
particles 0.25 inch in diameter. (Round your answer to two decimal places.)
a. | About 0.91 mi/h | b. | About 0.26 mi/h | c. | About –0.09
mi/h | d. | About 0.56 mi/h | e. | About 0.41 mi/h |
|
|
|
18.
|
Use the fact that the resistance of a wire carrying
an electrical current is directly proportional to its length and inversely proportional to its
cross-sectional area.
If #28 copper wire (which has a diameter of 0.0126 inch) has a
resistance of 64.17 ohms per thousand feet, what length of #28 copper wire will produce a resistance
of 33.5 ohms?
a. | About 522 mi/h | b. | About 517 mi/h | c. | About 507
mi/h | d. | About 527 mi/h | e. | About 537 mi/h |
|
|
|
19.
|
The frequency of vibrations of a piano string
varies directly as the square root of the tension on the string and inversely as the length of the
string. The middle A string has a frequency of 400 vibrations per second. Find the frequency of a
string that has 1.35 times as much tension and is 1.4 times as long.
a. | 361.97 vibrations / sec | b. | 331.97 vibrations / sec | c. | 341.97 vibrations
/ sec | d. | 371.97 vibrations / sec | e. | 351.97 vibrations / sec |
|
|
|
20.
|
The electrical resistance, R, of a wire is
directly proportional to its length, l, and inversely proportional to the square of its
diameter, d. A wire 80 meters long of diameter 4 millimeters has a resistance of 10
ohms. Find the resistance of a wire made of the same material that has a diameter of 3 millimeters
and is 45 meters long.
|