Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Select the order for the following
matrix.
|
|
|
2.
|
Select the augmented matrix for the system of
linear equations.
|
|
|
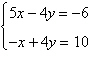
3.
|
Fill in the blank(s) using elementary row
operations to form a row-equivalent matrix.
|
|
|
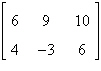
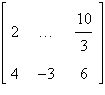
4.
|
Determine the order of the matrix.
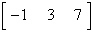
a. | 1 ´
1 | b. | 3 | c. | 3 ´ 3 | d. | 3 ´ 1 | e. | 1 ´ 3 |
|
|
|
5.
|
Identify the elementary row operation being
performed to obtain the new row-equivalent matrix.
Original Matrix | New
Row-Equivalent Matrix | | | | |
a. | Add 2 times R1 to
R2. | b. | Add –2 times
R1 to R2. | c. | Add 2 times
R2 to R1. | d. | Add –2 times
R2 to R1. | e. | Add 2 times
R1 to R1. |
|
|
|
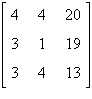
6.
|
Use the matrix capabilities of a graphing utility
to write the matrix in reduced row-echelon form.
|
|
|
7.
|
Find  .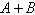
|
|
|
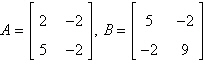
8.
|
Use the matrix capabilities of a graphing utility
to find AB, if possible.
|
|
|
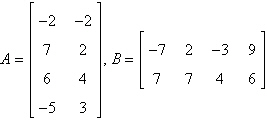
9.
|
Use the inverse formula  to find the inverse of the 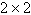 matrix (if it
exists).
|
|
|
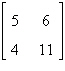
10.
|
Consider a person who invests in AAA-rated bonds,
A-rated bonds, and B-rated bonds. The average yields are 6.5% on AAA bonds, 7% on A bonds, and 9% on
B bonds. The person invests twice as much in B bonds as in A bonds. Let x, y and z
represent the amounts invested in AAA, A, and B bonds, respectively.
Total Investment | Annual Return | $12,000 | 890 | | |
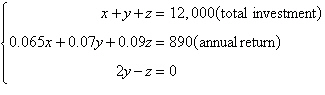
Use the inverse of the coefficient
matrix of this system to find the amount invested in each type of bond.
a. | $7000 in AAA-rated bonds
$2000 in A-rated bonds
$4000 in B-rated bonds | b. | $5000 in AAA-rated
bonds
$7000 in A-rated bonds
$3000 in B-rated bonds | c. | $5000 in AAA-rated bonds
$6000 in A-rated bonds
$4000 in B-rated
bonds | d. | $3000 in AAA-rated
bonds
$2000 in A-rated bonds
$6000 in B-rated bonds | e. | $6000 in AAA-rated bonds
$2000 in A-rated bonds
$4000 in B-rated
bonds |
|
|
|
11.
|
A small home business creates muffins, bones, and
cookies for dogs. In addition to other ingredients, each muffin requires 2 units of beef, 3 units of
chicken, and 2 units of liver. Each bone requires 1 unit of beef, 1 unit of chicken, and 1 unit of
liver. Each cookie requires 2 units of beef, 1 unit of chicken, and 1.5 units of liver. Find the
numbers of muffins, bones, and cookies that the company can create with the given amounts of
ingredients.
700 units of beef
650 units of chicken
625 units of
liver
a. | 150 muffins, 200 bones, 150 cookies
| b. | 150 muffins, 200 bones, 100 cookies
| c. | 200 muffins, 100 bones, 150 cookies
| d. | 100 muffins, 200 bones, 150 cookies
| e. | 100 muffins, 100 bones, 650 cookies
|
|
|
|
12.
|
Solve the system of linear
equations
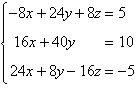 using an inverse
matrix.
|
|
|
13.
|
Find the determinant of the matrix by the method of
expansion by cofactors. Expand using the column 2.
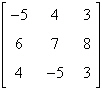
a. | –423 | b. | 423 | c. | –421 | d. | –422 | e. | –424 |
|
|
|
14.
|
Evaluate the determinant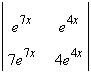 
in which the entries are functions.
|
|
|
15.
|
Find all minors of the matrix  .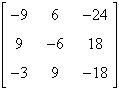
|
|
|
16.
|
Use Cramer’s Rule to solve (if possible) the
system of equations.
|
|
|
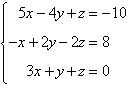
17.
|
Find y such that the points are
collinear.
|
|
|
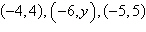
18.
|
Use a determinant to find an equation of the line
passing through the points.
|
|
|
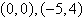
19.
|
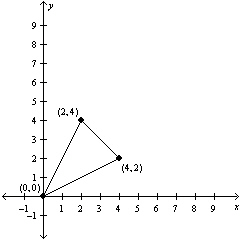
Use a determinant and the given vertices of a
triangle to find the area of the triangle.
|
|
|
20.
|
Use a determinant to find the area of the triangle
shown below.
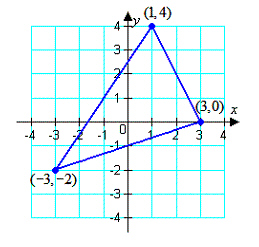
a. | 14 square units | b. | 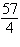 square units | c. |  square units | d. | 12 square units | e. |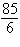 
square units |
|