Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Fill in the blank(s) using elementary row
operations to form a row-equivalent matrix.


|
|
|
2.
|
An augmented matrix that represents a system of
linear equations (in variables x, y, z and w if applicable) has been
reduced using Gauss-Jordan elimination. Find the solution represented by the augmented
matrix.
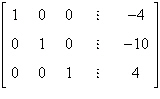
|
|
|
3.
|
Use matrices to solve the system of equations (if
possible). Use Gaussian elimination with
back-substitution or Gauss-Jordan
elimination.
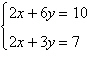
|
|
|
4.
|
Use the matrix capabilities of a graphing utility
to reduce the augmented matrix corresponding to the system of equations, and solve the
system.
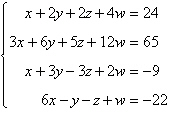
|
|
|
5.
|
Find 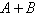 . .

|
|
|
6.
|
A corporation has four factories, each of which
manufactures sport utility vehicles and pickup trucks. The number of units of vehicle 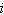 produced at factory
produced at factory  in one day is represented by in one day is represented by 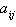 in the matrix
in the matrix
 . .
Find the production levels if
production is increased by 10%.
|
|
|
7.
|
Find x and y.
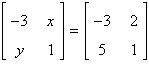
a. | x = 2, y = 5 | b. | x = 2, y = 2 | c. | x = –2, y = –5 | d. | x = 5, y = 2 | e. | x = –3, y = 1 |
|
|
|
8.
|
Use the inverse formula 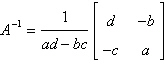 to find the inverse of the to find the inverse of the 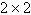 matrix (if it
exists). matrix (if it
exists).
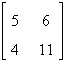
|
|
|
9.
|
Use the inverse formula 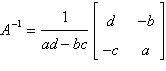 to find the inverse of the to find the inverse of the 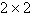 matrix (if it
exists). matrix (if it
exists).
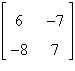
|
|
|
10.
|
Use the inverse formula 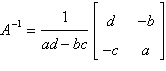 to find the inverse of the to find the inverse of the 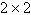 matrix (if it
exists). matrix (if it
exists).

|
|
|
11.
|
Consider a person who invests in AAA-rated bonds,
A-rated bonds, and B-rated bonds. The average yields are 6.5% on AAA bonds, 7% on A bonds, and 9% on
B bonds. The person invests twice as much in B bonds as in A bonds. Let x, y and z
represent the amounts invested in AAA, A, and B bonds, respectively.
Total Investment | Annual Return | $500,000 | 38,000 | | |
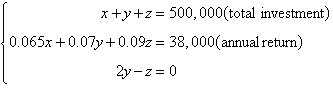
Use the inverse of the coefficient
matrix of this system to find the amount invested in each type of bond.
a. | $200,000 in AAA-rated bonds
$201,000 in
A-rated bonds
$100,000 in B-rated bonds | b. | $200,000 in
AAA-rated bonds
$100,000 in A-rated bonds
$200,000 in B-rated bonds
| c. | $201,000 in AAA-rated bonds
$100,000 in
A-rated bonds
$200,000 in B-rated bonds | d. | $101,000 in
AAA-rated bonds
$200,000 in A-rated bonds
$200,000 in B-rated bonds
| e. | $200,000 in AAA-rated bonds
$200,000 in A-rated
bonds
$99,000 in B-rated bonds |
|
|
|
12.
|
Find the inverse of the matrix 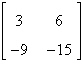 . .
|
|
|
13.
|
Solve the system of linear
equations
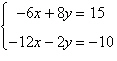
using the inverse matrix 
|
|
|
14.
|
Find the determinant of the matrix.
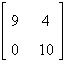
|
|
|
15.
|
Find the determinant of the matrix. Expand by
cofactors on the row or column that appears to make the computations easiest.

a. | –32 | b. | –30 | c. | –34 | d. | –33 | e. | –31 |
|
|
|
16.
|
Use the matrix capabilities of a graphing utility
to find the determinant of the matrix
 . .
a. | –48 | b. | 128 | c. | –64 | d. | –32 | e. | –384 |
|
|
|
17.
|
Use Cramer’s Rule to solve (if possible) the
system of equations.

|
|
|
18.
|
Find a value of y such that the triangle
with the given vertices has an area of 4 square units.

|
|
|
19.
|
Use a determinant and the given vertices of a
triangle to find the area of the triangle.
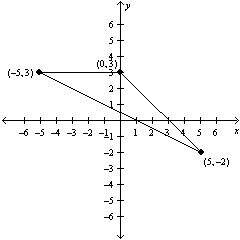
|
|
|
20.
|
Find the uncoded 1 ´
3 row matrices for the message "MERRY CHRISTMAS" by assigning a number to each
letter in the alphabet such as  and so on (with 0 assigned to a blank
space); and so on (with 0 assigned to a blank
space);
then encode the message using the encoding matrix 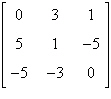 . .
|